Binomial Heap

Binomial Heap是由一群 Binomail Tree所組成的 Binomial Tree(BT)含有下列特性

高度為k的 BT共有2^k個node
高度為k的 BT可以看成 BT0~BTk-1的組合再加上一個root組成

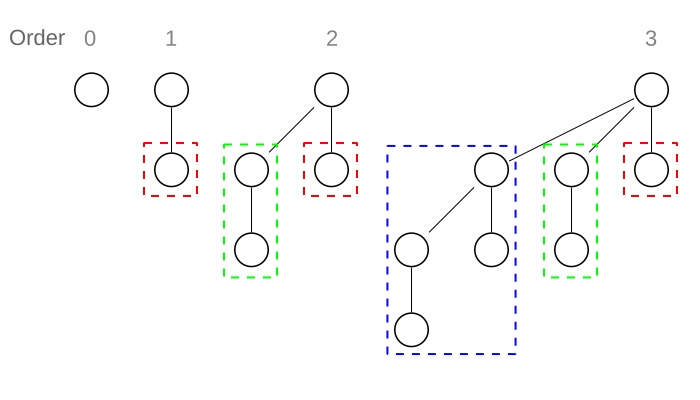
Binomial Heap

是 mergable heap
由一群 Binomial Tree組成，每個BT都滿足 min-heap的性質
對於高度為k的BT只能存在最多一棵
以二進位來看待的話，第K位就代表是否存在高度為K的BT
- 以下圖為例，就是11001 (右邊最小)
- 因此任何數量的結點都可以用不同的BT給組合出來

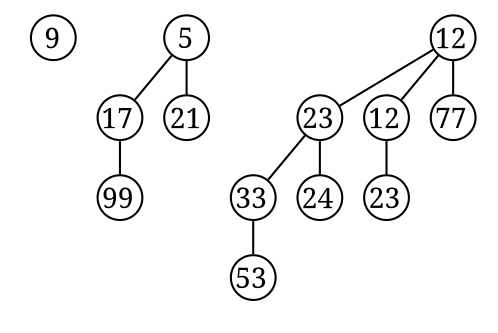
##Implement##

採用 Left-Child Right-sibling的方式來實現，左邊指向child,右邊指向同輩
value: node的值
degree: 以此node為root的BT的高度
parent: 指向其parent

class Node{
    public:
        Node* parent;
        Node* child;
        Node* sibling;
        int value;
        int degree;
        Node(){
            parent = NULL;
            child = NULL;
            sibling = NULL;
            value = 0;
            degree = 0;
        }
};

##Functions##

getMin
size
Travese (postorder)
mergeHeap
Insert
deleteMin

##getMin## 由於每個BT本身都已經是min-heap的特性了，因此只要針對每個BT的root比較其值即可

int getMin(){
  Node* x = head;
  int min = INT_MAX;
  while(x!=NULL){
    if(x->value < min)
    min = x->value;
    x = x->sibling;
  }
    return min;
}

##size## 由於 Binomial Heap內都是由 Binomial Tree組成，所以可以由每個BT的degree得到其node數量再把所有加總即可。

int size(){
    Node* tmp = head;
    int count=0;
    while(tmp){
        count+= (1<<tmp->degree);  // 2^degree
        tmp = tmp->sibling;
    }
    return count;
}

##Postorder## 這邊是每個BT都要獨立跑一次Postorder的結果，所以在遞迴的過程中要對root做一些控制

//對每一棵BT都跑一次postorder
void postorder(){
  Node* tmp = head;
  while(tmp){
    _postorder(tmp);
    tmp = tmp->sibling;
}
    printf("\n");
}

//用parent判斷是不是root,避免root跑去呼叫到別的BT
void _postorder(Node* node){
    if(!node)
        return;
    _postorder(node->child);
    if(node->parent)
        _postorder(node->sibling);
    printf("%d ",node->value);
}

##MergeHeap## 要合併兩個 Binomial Heap

先把兩個 Binomail Heap的 BT list給重新串接起來，以degree為key做sorting.
再根據這個新的BT list開始進行一系列的合併
如果只有兩個高度相同的BT，就直接合併
如果有三個高度相同的BT，就把後面兩棵合併(維持sorting)

void MergeHeap(BinomialHeap &bh){

    mergeHeap(bh);  //先把BT list給重新串接起來
    Node* prev = NULL;
    Node* x = head;
    Node* next = x->sibling;
    while(next){
        if( (x->degree != next->degree) || next->sibling && next->sibling->degree == x->degree){
            prev = x;  //前後兩棵BT的高度不同 或是 後面三棵BT的高度都相同
            x = next;  //那就把指標往前移動，下次再合併
        }
        else if( x->value <= next->value){  //前面BT的值比較小，所以後面的合併進來
            x->sibling = next->sibling;
            mergeTree(next,x);
        }
        else{ //前面那棵BT的值比較大，要往後合併，視情況也要更新 head指標
            if(!prev){
                head = next;                //更新head 指標
            }
            else{
                prev->sibling = next;
            }
            mergeTree(x,next);           //合併
            x = next;
        }
        next = next->sibling;
    }
}

要把兩個 Binomial Heap的BT list給重新串接起來，採用 merge sort的方法 螢幕截圖 2014-01-03 22.49.08.png

使用 newHead紀錄合併後的頭
使用 newCurr來紀錄每次合併後的尾

void mergeHeap(BinomialHeap &bh){
    Node* head2 = bh.head;
    Node* head1 = head;

    Node* newHead, *newCurr;

    if(!head1){            //如果本身是空的，就不需要合併，直接指向對方即可
        head = head2;
        return ;
    }
  else if(!head2){           //對方是空的，也不需要合併
    return ;
  }

    //先行尋找誰的開頭比較小，當做新串列的頭
    if(head1->degree > head2->degree){
        newHead = newCurr = head2;
        head2 = head2->sibling;
    }
    else {
        newHead = newCurr = head1;
        head1 = head1->sibling;
    }

    while(head1 && head2){
        if(head1->degree < head2->degree){
            newCurr->sibling = head1;
            newCurr = head1;
            head1 = head1->sibling;
        }
        else {
            newCurr->sibling = head2;
            newCurr = head2;
            head2 = head2->sibling;
        }

    }
    while(head1){
        newCurr->sibling = head1;
        newCurr = head1;
        head1 = head1->sibling;
    }
    while(head2){
        newCurr->sibling = head2;
        newCurr = head2;
        head2 = head2->sibling;
    }

    head = newHead;
}

合併兩個 Binomial Tree，由於我們是min-heap的特性，所以當兩棵高度相等的BT要合併時，根據root的值來決定誰是合併後的root.

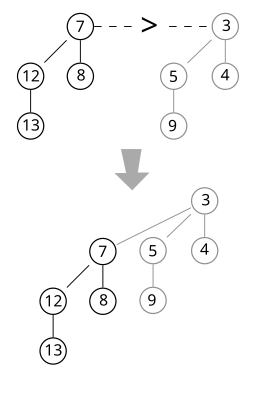
假設已經知道BT(y)的值比BT(z)還要大，所以BT(z)會是合併後的root

y的parent指到z
y的sibling 指到 z本來的child
z的child 指到y
z的degree 加一

void mergeTree(Node* y,Node* z){
    y->parent = z;
    y->sibling = z->child;
    z->child = y;
    z->degree++;
}

##Insert## 要插入一個新的元素，就是創見一個新的 Binomial Heap，然後跟原本的Heap執行合併即可

void insert(int value){
    BinomialHeap bh;
    bh.head = new Node();
    bh.head->value = value;
    MergeHeap(bh);
}

##Delete## 要從 BinomialHeap中刪除當前最小元素

先找到最小元素所在的那棵BT
把該BT從list裡面拔除
把該BT的children給反向排序(degree為key)
在跟原本的BT list合併

螢幕截圖 2014-01-03 23.02.35.png

void deleteMin(){
    int min = head->value;
    Node* tmp = head;
    Node* minPre = NULL;
    Node* minCurr = head;
    // 找到最小的node位於何處，由於要將該BT給拔除，所以必須要記得該BT前面那棵BT
    // 如果最小棵的是第一棵，那也要一併更新 head 指標
    while(tmp->sibling){
        if(tmp->sibling->value < min){
            min = tmp->sibling->value;
            minPre = tmp;
            minCurr = tmp->sibling;
        }
        tmp = tmp->sibling;
    }
    if(!minPre && minCurr) //最小棵是第一個
        head = minCurr->sibling;
    else if(minPre && minCurr)
        minPre->sibling = minCurr->sibling;

  //H' Make-BINOMIAL-HEAP()

    Node *pre,*curr;
    //用三個指標反轉一個 single link list
    pre = tmp = NULL;
    curr = minCurr->child;
    while(curr){
        tmp = curr->sibling;
        curr->sibling = pre;
        curr->parent = NULL;
        pre = curr;
        curr = tmp;
    }
    //創建一棵新的binomial heap,並且讓他的head 指向反轉後的BT list
  BinomialHeap bh ;
    bh.head = pre;
    //再度合併
    MergeHeap(bh);

}

圖片來自

Binomial Wiki
Introduction To Algorithms，Chapter 19 Binomial Heaps